Gompertz–Makeham law of mortality

Strategy

Axial: https://linktr.ee/axialxyz

Axial partners with great founders and inventors. We invest in early-stage life sciences companies such as Appia Bio, Seranova Bio, Delix Therapeutics, Simcha Therapeutics, among others often when they are no more than an idea. We are fanatical about helping the rare inventor who is compelled to build their own enduring business. If you or someone you know has a great idea or company in life sciences, Axial would be excited to get to know you and possibly invest in your vision and company. We are excited to be in business with you — email us at info@axialvc.com

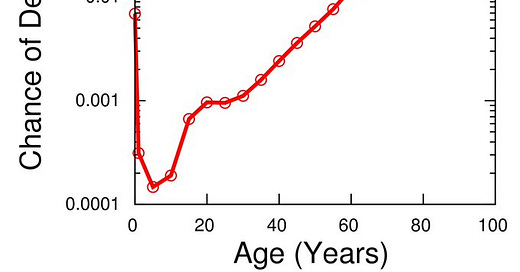
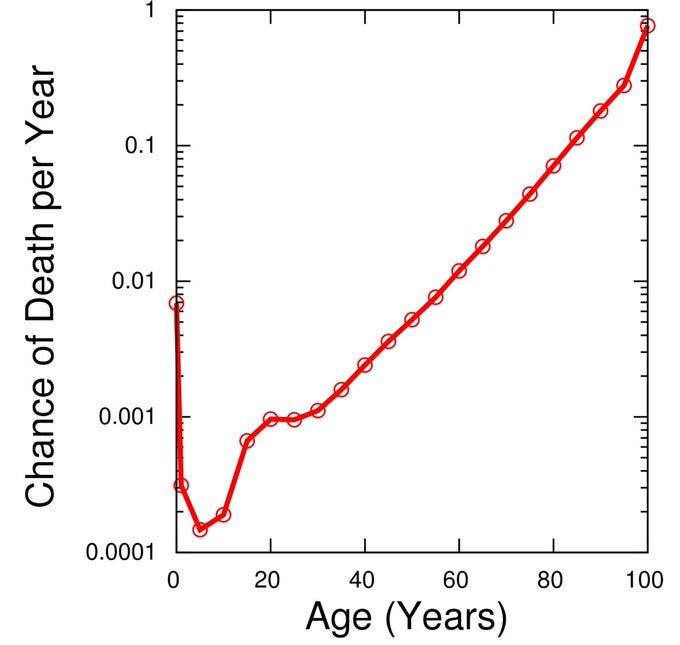
Gompertz–Makeham law of mortality is a mathematical model used to describe the age-specific mortality rates observed in human and other species. This model has played a significant role in actuarial science and has also been extensively studied in the field of biodemography and the biology of aging.

The origins of the law can be traced back to Benjamin Gompertz's seminal paper titled "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies," published in 1825 in the Philosophical Transactions of the Royal Society. Gompertz, a British actuary, proposed a model that described the exponential increase in mortality rates with age, which later became known as the Gompertz law of mortality. This equation is represented as:

μ(x) = α · eβx

Where μ(x) is the mortality rate at age x, and α and β are constants representing the baseline mortality rate and the rate of increase in mortality with age, respectively.

In 1860 and 1867, William Makeham, another British actuary, extended Gompertz's model by adding a constant term to account for age-independent mortality, leading to the Gompertz-Makeham equation:

μ(x) = α · eβx + γ

In this formulation, γ represents the age-independent mortality rate, often referred to as the "extrinsic" or "background" mortality rate, which is assumed to be constant across all ages.

The Gompertz-Makeham law has been widely used in actuarial science for calculating life contingencies, such as annuities and life insurance premiums. It provides a mathematical framework for estimating the probability of survival or death at different ages, which is crucial for determining the appropriate pricing and risk assessment for these financial products.

Actuaries have extensively studied and refined the parameters of the Gompertz-Makeham equation to accurately model mortality patterns observed in various human populations. By analyzing large datasets of mortality records, they can estimate the values of α, β, and γ that best fit the observed data and use these estimates to make predictions about future mortality rates and life expectancies.

While the Gompertz-Makeham law was initially developed for human populations, its application has extended to the field of biodemography, where it has been used to study mortality patterns across different species and populations. Comparative studies have analyzed the values of the parameters α, β, and γ for various species, providing insights into their aging processes and potential differences in intrinsic and extrinsic mortality factors.

One notable contribution in this area was made by George Sacher, a biophysicist at the Argonne National Laboratory. In the 1950s and 1960s, Sacher applied the Gompertz model to compare mortality patterns across different mammalian species, introducing the concept of the "mortality rate doubling time," which is calculated as ln(2)/β. This measure allows for direct comparisons of the rates of aging between species, with shorter doubling times indicating faster aging processes.

The Gompertz-Makeham law has inspired researchers to seek biological interpretations and explanations for the observed patterns of mortality. One approach has been to apply concepts from reliability theory, which deals with the failure kinetics of engineered systems with redundant components. To model the reinforcing mechanisms that cause phenotypes of aging.

Researchers such as Leonid Gavrilov and Natalia Gavrilova have developed models based on reliability theory to explain the exponential increase in mortality rates described by the Gompertz term. These models assume that organisms consist of redundant functional units or components, and the failure of these components over time leads to an increasing probability of mortality.

Other researchers, like E. Michael Milne, have proposed alternative models, such as the "nested binomial model," which assume that organisms comprise a set of functions connected in series, and the failure of any single function results in death. These models aim to provide a mechanistic understanding of the aging process and the underlying causes of the observed mortality patterns. Overall, the Gompertz law is an exponential. Various factors (i.e. aging phenotypes) compounding overtime affecting large ensembles of cells (i.e. tissue/organ failure). As a natural log (e=2.7, governing a lot of natural phenomena), the law increases by 2.7 every ~7 years. Every decade or so, it becomes >2.7x harder to drug aging. Therapies like bend this curve need a >10x-100x effect on a phenotype. For longevity medicines, 20%-50% gains are probably not enough, unless they can synergize.

While the Gompertz-Makeham law has been widely adopted and studied, it has limitations and does not fully capture the complexity of mortality patterns observed in all populations and at all ages. One notable limitation is the phenomenon of late-life mortality plateaus or deceleration observed in some species, including humans. At advanced ages, the mortality rates often deviate from the exponential increase predicted by the Gompertz term, exhibiting a plateau or even a decline in mortality rates. This phenomenon has been attributed to factors such as population heterogeneity, where the most robust individuals tend to survive to the oldest ages, or biological mechanisms that may slow the aging process at extreme ages.

To address these limitations, researchers have proposed various extensions and alternative models, such as the logistic model, the Weibull model, and the Heligman-Pollard model. These models aim to better capture the observed mortality patterns, particularly at advanced ages, and provide a more comprehensive understanding of the underlying biological processes.

The study of mortality patterns and the Gompertz-Makeham law continues to be an active area of research, with ongoing efforts to refine and extend the models and to integrate them with emerging insights from various fields, including genetics, systems biology, and computational modeling. One area of interest is the integration of genetic and molecular data to better understand the underlying mechanisms driving the observed mortality patterns. By combining biodemographic data with genomic, proteomic, and metabolomic information, researchers aim to unravel the complex interactions between genetic factors, environmental influences, and the aging process.

Additionally, the advent of big data and advanced computational techniques has opened new avenues for analyzing and modeling mortality patterns. Machine learning algorithms and simulation models can be employed to identify complex patterns, test hypotheses, and generate predictions that can inform actuarial practices, public health policies, and our understanding of the biology of aging. The Gompertz-Makeham law of mortality has played a pivotal role in actuarial science, biodemography, and the study of aging. While it has limitations, it continues to serve as a foundational model and a starting point for exploring the intricate patterns of mortality across species and populations. As scientific knowledge advances, the integration of diverse data sources and analytical techniques holds the promise of refining and extending our understanding of the fundamental processes governing life and death.